Users and instrument makers worldwide rely on metrology software to help them improve their products or understand material properties. At Digital Surf, we are responsible for providing them with accurate and compliant results. However, proving that an algorithm is correct is not so straightforward. François Blateyron, senior expert on surface metrology, discusses this complex issue.
Users tend to compare the results they get with other sources, other commercial software packages or so-called “reference software” results provided by National Metrology Institutes (NMI). But when results differ, which ones can be trusted? A recent study shows that NMI software packages1 do not provide comparable results for common parameters and do not cover all parameters and filters. Therefore, they cannot be used as a reference by everyday users.

Towards an independent reference
There is a strong need for an independent reference that would not put too many constraints on the production of algorithms but would allow developers to measure the accuracy of their implementations. Developers should remain free to make their own implementation, their own optimizations for speed (or their own approximations when the program runs on less powerful hardware.)
Such independent references can only be provided by Nature and in particular, Maths. Most parameters are now defined for the continuous case by an equation. By defining a surface or a profile (a studiable) also as an equation and combining with the parameter equation, a resulting formal equation for the reference parameter value can be calculated that is highly accurate. For example, a simple sine wave profile can be defined as:
z(x)=A sin(x)
with A the half amplitude and x∈[0;2nπ]. We can set the length L to be a multiple of the chosen period, all in the same unit (for example, µm). The parameter can then be calculated, for example by substituting the surface equation into the parameter equation:
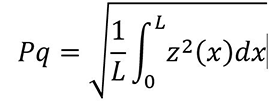
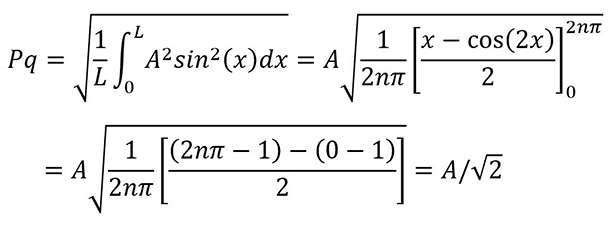
In order to test the parameter algorithm alone, it is tested without filter, without leveling or any other operation. Filters and form removal are tested separately, and the full process is taken as a series of black boxes, each tested independently with a mathematical reference.
This means that Pq=Pt/(2√2) for a sine wave (A=Pt/2) and that it is independent from the period. For example, for an amplitude Pt=1µm, we should obtain Pq≈0.353553µm and the result can be calculated with as many decimal places as needed.
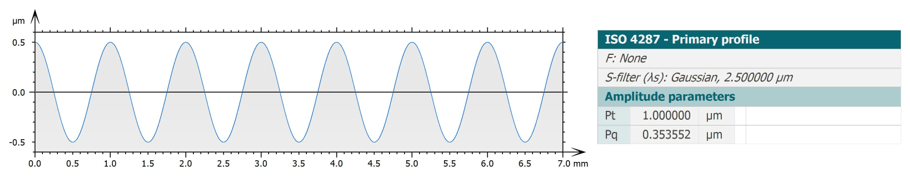
The accuracy of the parameter calculation in a software package depends, of course, not only on the algorithm but also on the number of points in X and digitization in Z of the discrete profile. So, discrete studiables generated for the purpose of validation should introduce the least amount of uncertainty and allow the evaluation of the sole contributions of the algorithm to the final uncertainty (or deviation).
Generalizing mathematical reference values
For several years, Digital Surf has invested in research on new methods to validate parameters and filters. In collaboration with the University of Nottingham and the National Physical Laboratory (UK), we work to develop reference pairs for each parameter from common standards. A reference pair is 1) a definition of a mathematical studiable paired with 2) a formal expression of the parameter when calculated on the given studiable.
This mathematically intensive work allowed Digital Surf to validate field parameters from ISO 251782 and more recently profile parameters from ISO 21920 (and by extension from ISO 4287 and ISO 13565) and the Gaussian filter3. This work allowed Digital Surf to validate and improve Mountains® algorithms and identify which parameters are sensitive to which characteristics.
Areal parameters
Several synthetic surface equations were defined, from simple sine waves in X and Y to Bernouilli or Chebychev polynomials with various orders, and their corresponding equations were passed through each parameter definition, to obtain the formal resulting equation. Then a numeric approximation was calculated, by assigning a value to the various equation terms (amplitude, polynomial coefficients etc.) to obtain a value to which the value calculated in Mountains® could be compared. Then, a discrete version of the surface was generated at various resolutions and loaded into Mountains® to calculate the parameters and obtain deviations. Below is an example of results for the “4-term cosine” surface. The accuracy is usually better than ±0,001% on large surfaces, which is more than necessary for most metrological results.
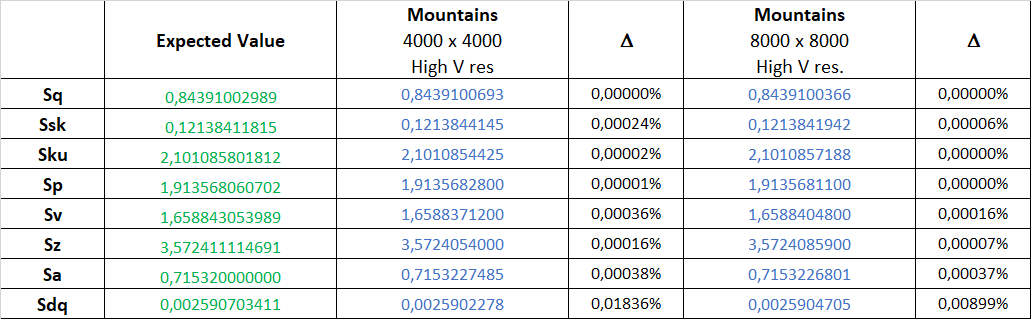
It was not always possible to obtain the formal expression of all parameters with all surface equations, as some calculations were too complex. But in the end, it was possible to validate all field parameters, including slope (Sdq), developed area (Sdr), material ratio (Smc, Smr) with derived families, Sk, Spk, Svk etc. and volume parameters Vmp, Vmc, Vvc, Vvv.
A test on various Abbott curve shapes, suitable for the calculation of functional parameters was carried out (see below).

A dozen shapes were generated from the same polynomial equation and material ratio parameters were tested for different points on the curve:
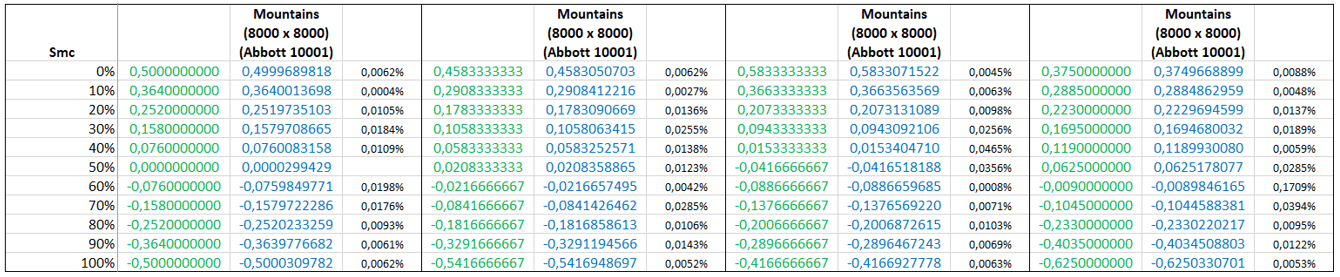
Functional parameters, were also validated.

In most cases, deviation was always below 0.1% and usually much less.
The trickiest parameters were those based on autocorrelation (Sal, Str) where synthetic equations had to be generated in the autocorrelation domain instead of the space domain. This required a special test procedure in the source code of Mountains® to validate the thresholding at s=0.2 and the accurate calculation of the smallest and largest radius on the autocorrelation lobe. By varying the equation, it was possible to generate lobes that were oblong or round, thin or large and test algorithm robustness.
So far, the missing references are for Feature parameters which are based on a topological algorithm instead of a linear equation. The only solution here is to carry out a code review to ensure that the algorithm is correctly implemented. Reference values will be necessary in the future for these parameters as well.
Profile parameters
Following the first 4-year research work focusing on areal parameters, an extension was agreed during Luke Todhunter’s post-doc year to apply the same method to profile parameters (those defined in ISO 21920) and also to the Gaussian filter3 (profile and areal) and form fitting, including leveling.
Conclusion
Users have legit questions and expectations on the compliance and accuracy of parameter results provided by Mountains®. Thanks to the method developed over the last four years, we now have the tools to validate most areal and profile parameters. Ideally, an official certification for our software, similar to a UKAS or DKD certificate, would be necessary but this is not yet possible (only instruments and material measures can be certified). However, we can provide the necessary mathematical background for our algorithms.
Mountains® is not only the most complete surface metrology software package, it is also the most accurate and compliant.
1Todhunter L, Leach R K, Lawes S D A, Blateyron F, 2017, An analysis of Type F2 software measurement standards for profile surface texture parameters, Measurement Science and Technology, 28(6).
2Todhunter L, Leach R K, Lawes S D A, Blateyron F, Harris P, 2018, Development of mathematical reference standards for the validation of surface texture parameter calculation software, Journal of Physics, conference series, 1065(8).
3Todhunter L, Leach R K, Blateyron F, 2020, Mathematical approach to the validation of surface texture filtration software, Euspen 20th international conference, Geneva.
Author : François Blateyron